Damage Analysis of Elastic Modulus of Composites by Stitching Diameter
Sinoma Science & Technology Co., Ltd., Nanjing 210012
0 引言
缝合复合材料通过在厚度方向引入缝线,明显改善和提高了层合板的损伤阻抗、损伤容限和层间断裂韧性,具有广泛的应用前景[1-6]。准确预测缝合复合材料的力学性能是其应用和发展的前提。但是缝线的加入导致了缝合复合材料细观结构非常复杂、失效模式多样,也使得对其面内力学性能的预测变得更加困难[7-9]。目前国内外众多研究机构和学者致力于缝合复合材料力学性能预测研究。I.Verpoest[10]针对缝线处及周围的富树脂区建立了几何模型,并选取Tsai-Hill准则来确定模型中单元是否失效,并利用细观模型得到准则中的性能参数。A.Margossian [11]采用有限元软件PAM-Form模拟了织物局部缝合的缝合过程,发现有限元模型可用于确定接缝对成形行为的影响,因此优化了缝合工艺。金春花等[12]以正八边形棱柱代替缝线,单胞有限元模型上施加的是周期性边界条件,使得计算结果更加合理和准确。于芳等[13]对比分析缝合复合材料弹性常数的细观力学模型,发现假设纤维在针脚附近只有部分纤维发生弯曲的模型对缝纫参数改变敏感,且得到结论更合理。李晨等[14-15]建立缝合单向板的三维有限元分析模型,考虑了缝合导致纤维面内和面外弯曲,结果表明模型能很好预测缝合单向板拉伸和压缩性能。目前的研究大多是对单向布、平纹布的二维有限元预报,而对缎纹织物三维有限元研究较少,因此进一步深入分析和验证缝线粗细对缝合碳纤维缎纹织物增强复合材料的面内弹性模量的影响规律具有很强的理论和工程应用价值。本文主要介绍了缝线粗细对复合材料面内弹性模量的损伤分析。
1 有限元3D模型的构建
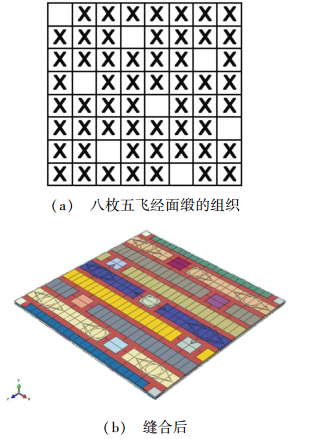
根据八枚五飞经面缎的组织结构图 1(a)构建了典型单层三维单胞模型,其中模型三维尺寸为26.4 mm×26.4 mm×0.4 mm,碳纤维MT300作为缝线,每束编织纤维截面由矩形和两个椭圆形组成,基布上下表面的浮线忽略。图 1(b)为缝合的单胞模型。
2 有限元预报面内弹性模量
2.1 单层板的弹性常数预报
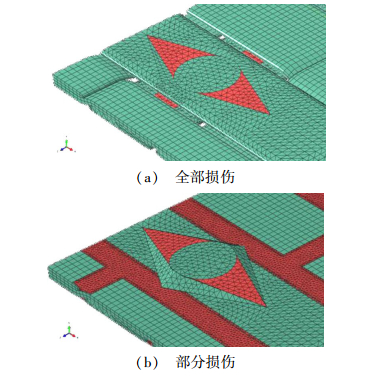
针对缝合密度10 mm×10 mm,缝线等效半径分别为0.64、0.586、0.36、0.32、0.293、0.18、0.10 mm,假设缝线截面为圆形,在缝线线宽处预报全部损伤和部分损伤两种情况(图 2)。
全部损伤模型是指由于缝线导致将缝合处纤维或断裂或挤向两边,但未挤出面外,如图 2(a)所示;部分损伤模型是指由于缝合导致缝线将缝合处纤维部分断裂、部分挤向两边并挤出面外,同时在缝线两端形成无纤维三角形区(树脂区),如图 2(b)所示。
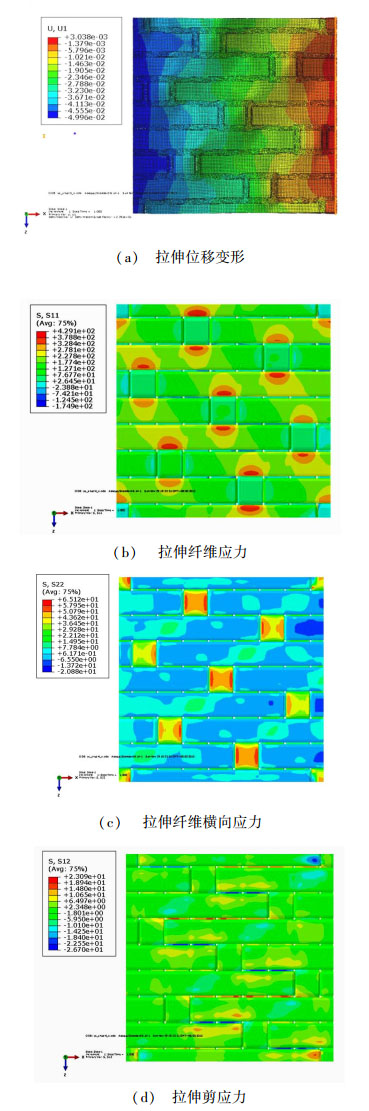
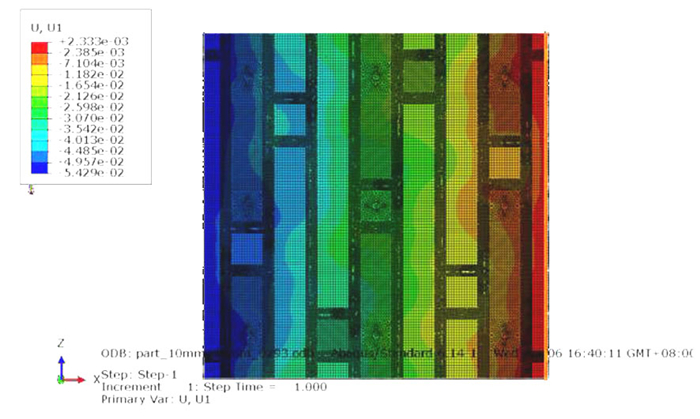
利用ABAQUS有限元软件对不同缝线直径的单层板的面内弹性模量进行预报。以0.293 mm为例,在x轴向施加拉伸载荷,求得模型在x轴方向应变ε1,则x向模量为E1;在z轴向施加拉伸载荷,求得模型在z轴方向应变为ε2,则z向模量为E2。在四边施加面剪切力50 MPa,求得胞元模型的平均剪应变为ε12,则其面内剪切模量为G12。其未损伤和损伤模型以及两种情况的变形如图 3~5所示。
通过有限元预报得出单胞模型的基本力学性能常数:面内弹性模量(E1和E2)、面内剪切模量(G12)和泊松比(ν12),依据有限元预报的单胞模型的基本力学常数,按照公式(1)~(5)可获得单层弹性常数,其他不同缝线直径的单层板均按照此方法进行有限元预报得出单层弹性常数。
|
$
{Q_{11}} = \frac{{{E_1}}}{{1-{v_{12}}{v_{21}}}}
$
|
(1) |
|
$
{Q_{12}} = \frac{{{v_{12}}{E_1}}}{{1-{v_{12}}{v_{21}}}}
$
|
(2) |
|
$
{Q_{21}} = \frac{{{v_{12}}{E_1}}}{{1-{v_{12}}{v_{21}}}}
$
|
(3) |
|
$
{Q_{22}} = \frac{{{E_2}}}{{1-{v_{12}}{v_{21}}}}
$
|
(4) |
|
$
{Q_{66}} = {G_{12}}
$
|
(5) |
2.2 层合板理论计算面内弹性模量
根据缝合工艺设计了循环铺层[0°/+45°/90°/-45°]并预报单层工程常数,按照经典层合板理论,不同直径缝线的层合板的等效工程常数有限元预报结果见表 1。
表 1 等效工程常数预报结果
Table 1 Prediction results of equivalent engineering constants
| 缝线半径/mm |
缝合状况 |
E/GPa |
Ex/GPa |
Ey/GPa |
Gxy/GPa |
νxy |
| 0.1 |
全部损伤 |
47.6 |
33.5 |
33.5 |
10.9 |
0.54 |
| 部分损伤 |
47.6 |
33.5 |
33.5 |
10.9 |
0.54 |
| 0.18 |
全部损伤 |
47.3 |
33.3 |
33.3 |
10.8 |
0.54 |
| 部分损伤 |
47.6 |
33.5 |
33.5 |
10.9 |
0.54 |
| 0.293 |
全部损伤 |
47.1 |
33.2 |
33.2 |
10.8 |
0.54 |
| 部分损伤 |
47.3 |
33.4 |
33.4 |
10.9 |
0.53 |
| 0.32 |
全部损伤 |
46.9 |
33.1 |
33.1 |
10.7 |
0.54 |
| 部分损伤 |
47.1 |
33.3 |
33.3 |
10.8 |
0.53 |
| 0.36 |
全部损伤 |
46.6 |
32.9 |
32.9 |
10.7 |
0.54 |
| 部分损伤 |
47.1 |
33.3 |
33.3 |
10.8 |
0.53 |
| 0.586 |
全部损伤 |
45.5 |
32.2 |
32.2 |
10.4 |
0.55 |
| 部分损伤 |
46.9 |
33.2 |
33.2 |
10.9 |
0.53 |
| 0.64 |
全部损伤 |
42.1 |
30.3 |
30.3 |
10.0 |
0.51 |
| 部分损伤 |
46.6 |
33.0 |
33.0 |
10.8 |
0.53 |
| 原始未缝合 |
46.2 |
32.5 |
32.5 |
10.2 |
0.59 |
由表 1可以看出,随着缝线变粗,在全部损伤状态下复合材料的拉伸和剪切模量略有降低;部分损伤状态下,模量变化很小,而缝合工艺使泊松比降低;同时较细的缝线在两种状态下相对于未缝合均略有提高,这可能是由于夹杂效应的原因。缝合总体而言并未对复合材料面内剪切强度产生太大影响;采用细缝线(半径R<0.3 mm时),对提高复合材料板面内弹性模量有利,但影响有限(≤9.5%)。综上,缝合对碳布中纤维的损伤影响很小。
3 实验验证
为验证有限元预报的有效性,实验按照有限元预报设计的参数制备缝合预制件,采用RTM工艺制备了缝合预制体复合材料试样,分别进行了力学性能测试。拉伸性能测试参照GB/T 1447—2005纤维增强塑料拉伸性能试验方法进行,采用位移加载控制,加载速度2 mm/min;所有试样在MTS Landmark动、静态加载试验机上完成,然后按照模量计算公式得到的拉伸强度和模量如表 2所示。分析表 2数据可以看出:缝合密度10 mm×10 mm时,不同粗细的缝线复合材料面内弹性模量变化较小,较细缝线的弹性模量出现最大值,缝合总体而言并未对复合材料面内模量产生太大影响;实验结果的规律与预报相一致,但是实验结果的数值比预报值高,可能是缝线对基布损伤模型所假设的两种极端状态有偏差,导致实验值相对较大;从预报值和实验值可知,缝线粗细对缝合复合材料拉伸模量的影响规律一致,缝线粗细对复合材料面内模量影响不大,无论有限元预报结果还是实验结果均反映了这一现象。
表 2 不同粗细缝线的拉伸模量实验结果
Table 2 Experimental results of elastic modulus on variation of different diameter
| 项目 |
模量/GPa |
| R=0.18 mm |
R=0.254 mm |
R=0.293 mm |
R=0.328 mm |
| 平均值 |
37.3 |
38.0 |
37.6 |
37.5 |
| 离散度/% |
2.3 |
4.8 |
2.1 |
4.0 |
4 结论
(1) 在10 mm×10 mm的缝合密度下,缝线粗细总体而言并未对复合材料的面内强度产生太大影响,而且对最终复合材料泊松比的影响不大;采用细线对提高复合材料板面内弹性模量有利,但影响有限;当缝线细到一定程度后(半径R<0.3 mm时),缝合对碳布中纤维的损伤对面内弹性模量影响很小。
(2) 缝线粗细对复合材料的面内弹性模量影响不大的规律在实验和预报两个方面结果显示一致,为以后的研究简化奠定了基础。