2. 同济大学航空航天与力学学院, 上海 200092
2. Schoolof Aerospace Engineering and Applied Mechanics, Tongji University, Shanghai 200092
功能梯度材料是一种多相材料,其材料宏观特性在空间位置上呈梯度变化,消除了材料的物理性能突变现象,达到缓和热应力、避免或降低应力集中,优化结构整体使用性能的目的[1-3]。基于以上特点,功能梯度材料在航空航天、土木工程、机械、电磁、核工程、军事、生物医学等技术领域已有越来越广泛的应用。
对于功能梯度结构(梁、板、壳等)弹性问题的求解,主要的分析方法有解析法和数值法两大类。其中基于精确弹性理论的解析法是严格求解问题的控制方程和边界条件,目前仅对特定的问题有效。KASHTALYAN[4]得到了梯度呈指数分布的四边简支功能梯度矩形板弯曲问题弹性解。仲和尚[5]获得了四边简支功能梯度矩形板三维封闭解,其中材料常数沿厚度方向呈指数函数变化,线性分布和倒数分布。YANG, DING和CHEN[6]研究了横观各向同性对边简支功能梯度矩形板弯曲问题。OOTAO和ISHIHARA[7]获得了一种具有分段指数分布的功能梯度矩形板瞬态热弹性问题三维解。ABALI等[8]研究了四边简支功能梯度矩形板在点荷载作用下弯曲问题。周凤玺等[9]采用数值方法求解了材料常数按幂率变化的四边简支矩形板在热冲击下的热响应。余莲英等[10]采用弹性力学逆解法,求得了功能梯度曲梁在端部受弯矩作用解析解。WOODWARD和KASHTALYAN[11]研究了功能梯度矩形夹芯板在横向荷载作用下的弯曲问题。杨智勇、牛忠荣和程长征等[12]采用插值矩阵法直接对常微分方程组边值问题进行求解,得到了功能梯度材料矩形板三维位移、应力场的半解析解。PRADHAN和CHAKRAVERTY[13]利用经典板理论研究了功能梯度材料矩形板在不同的边界条件下的静力问题。MANTARI, RAMOS和CARRERA[14]利用新的非多项式位移分析了功能梯度板和夹芯板的静力问题。但关于一般幂函数分布的功能梯度矩形板三维问题解析解并没有获得。
本文从三维弹性理论出发,考虑材料常数沿厚度方向呈幂函数分布,引入PLEVAKO[15]解,获得了功能梯度矩形板在任意荷载作用下弯曲问题的弹性解。并给出算例,讨论了非均匀参数的变化对板应力和位移场的影响。
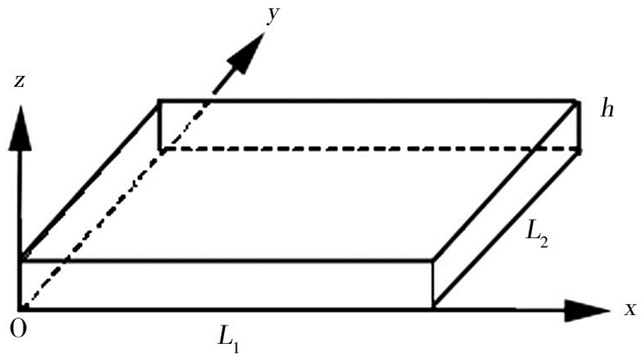
1 问题的描述和基本方程四边简支的功能梯度材料矩形板,其边长分别为L1、L2,厚度为h,引入xyz坐标系,0≤x≤L1,0≤y≤L2,0≤z≤h,如图 1所示。
|
| 图 1 功能梯度材料矩形板示意图 Figure 1 schematic of a functionally graded rectangular plate |
在不计体力的情况下,各向同性功能梯度三维矩形板,以位移表示的平衡方程为[16]:
| $ \begin{array}{l} E\left( z \right){\nabla ^2}u + \frac{{E\left( z \right)}}{{1 - 2\nu }}\frac{{\partial e}}{{\partial x}} + \left( {\frac{{\partial u}}{{\partial z}} + \frac{{\partial w}}{{\partial x}}} \right)\frac{{{\rm{d}}E\left( z \right)}}{{{\rm{d}}z}} = 0\\ E\left( z \right){\nabla ^2}v + \frac{{E\left( z \right)}}{{1 - 2\nu }}\frac{{\partial e}}{{\partial y}} + \left( {\frac{{\partial v}}{{\partial z}} + \frac{{\partial w}}{{\partial y}}} \right)\frac{{{\rm{d}}E\left( z \right)}}{{{\rm{d}}z}} = 0\\ E\left( z \right){\nabla ^2}w + \frac{{E\left( z \right)}}{{1 - 2\nu }}\frac{{\partial e}}{{\partial z}} + e\frac{{\rm{d}}}{{{\rm{d}}z}}\left[ {\frac{{2E\left( z \right)\nu }}{{1 - 2\nu }}} \right] + 2\frac{{\partial w}}{{\partial x}}\frac{{{\rm{d}}E\left( z \right)}}{{{\rm{d}}z}} = 0 \end{array} $ | (1) |
式中,x, y, z是笛卡儿坐标系,u, v, w是位移分量,e=∂u/∂x+∂v/∂y+∂w/∂z是体积应变,∇2=∂2/∂x2+∂2/∂y2+∂2/∂z2是拉普拉斯算子;E和ν分别是弹性模量和泊松比,它们都是关于坐标z的函数。
板上下表面的边界条件:
| $ \begin{array}{l} z = 0,{\sigma _z} = {Z_0}\left( {x,y} \right),{\tau _{xz}} = {X_0}\left( {x,y} \right),{\tau _{yz}} = {Y_0}\left( {x,y} \right)\\ z = h,{\sigma _z} = {Z_1}\left( {x,y} \right),{\tau _{xz}} = {X_1}\left( {x,y} \right),{\tau _{yz}} = {Y_1}\left( {x,y} \right) \end{array} $ | (2) |
式中,Z0(x, y),Z1(x, y),X0(x, y),X1(x, y),Y0(x, y),Y1(x, y)分别是上下表面作用的横向和切向荷载。
在四边简支边上,有:
| $ \begin{array}{l} {\sigma _x} = v = w = 0\;\;\;\;\;\left( {x = 0,a} \right)\\ {\sigma _y} = u = w = 0\;\;\;\;\;\left( {y = 0,b} \right) \end{array} $ | (3) |
问题的关键就是在边界条件(2)和(3)下求解控制方程(1)。
2 问题的求解根据PLEVAKO解[15],位移分量可以用两个函数L=L(x, y, z)和N=N(x, y, z)表示如下:
| $ \begin{array}{l} u = - \frac{{1 + v}}{E}\left( {\nu {\nabla ^2} - \frac{{{\partial ^2}}}{{\partial {z^2}}}} \right)\frac{{\partial L}}{{\partial x}} + \frac{{\partial N}}{{\partial y}}\\ v = - \frac{{1 + v}}{E}\left( {\nu {\nabla ^2} - \frac{{{\partial ^2}}}{{\partial {z^2}}}} \right)\frac{{\partial L}}{{\partial y}} - \frac{{\partial N}}{{\partial x}}\\ w = - 2\frac{{1 + v}}{E}\left( {{\nabla ^2} - \frac{{{\partial ^2}}}{{\partial {z^2}}}} \right)\frac{{\partial L}}{{\partial z}} + \\ \frac{\partial }{{\partial z}}\left[ {\frac{{1 + v}}{E}\left( {\nu {\nabla ^2} - \frac{{{\partial ^2}}}{{\partial {z^2}}}} \right)L} \right] \end{array} $ | (4) |
式中,L=L(x, y, z)和N=N(x, y, z)满足下面两个变系数的偏微分方程:
| $ {\nabla ^2}\left( {\frac{1}{E}{\nabla ^2}L} \right) - \frac{1}{{1 - v}}\left( {{\nabla ^2} - \frac{{{\partial ^2}}}{{\partial {z^2}}}} \right)L\frac{{{{\rm{d}}^2}}}{{{\rm{d}}{z^2}}}\left( {\frac{1}{E}} \right) = 0 $ | (5) |
| $ {\nabla ^2}N + \frac{{E'}}{E}\frac{{\partial N}}{{\partial z}} = 0 $ | (6) |
式中,E′=dE/dz。
应力分量也可以用函数L=L(x, y, z)和N=N(x, y, z)表示:
| $ {\sigma _x} = \left( {\nu \frac{{{\partial ^2}}}{{\partial {y^2}}}{\nabla ^2} - \frac{{{\partial ^4}}}{{\partial {x^2}\partial {z^2}}}} \right)L + \frac{E}{{1 + \nu }}\frac{{{\partial ^2}N}}{{\partial x\partial y}} $ |
| $ {\sigma _y} = \left( {\nu \frac{{{\partial ^2}}}{{\partial {x^2}}}{\nabla ^2} + \frac{{{\partial ^4}}}{{\partial {y^2}\partial {z^2}}}} \right)L - \frac{E}{{1 + \nu }}\frac{{{\partial ^2}N}}{{\partial x\partial y}} $ |
| $ {\sigma _z} = {\left( {\frac{{{\partial ^2}}}{{\partial {x^2}}} + \frac{{{\partial ^2}}}{{\partial {y^2}}}} \right)^2}L $ |
| $ \begin{array}{l} {\tau _{yz}} = - \left( {\frac{{{\partial ^2}}}{{\partial {x^2}}} + \frac{{{\partial ^2}}}{{\partial {y^2}}}} \right)\frac{{{\partial ^2}L}}{{\partial y\partial z}} - \frac{E}{{2\left( {1 + \nu } \right)}}\frac{{{\partial ^2}N}}{{\partial x\partial z}}\\ {\tau _{xz}} = - \left( {\frac{{{\partial ^2}}}{{\partial {x^2}}} + \frac{{{\partial ^2}}}{{\partial {y^2}}}} \right)\frac{{{\partial ^2}L}}{{\partial x\partial z}} + \frac{E}{{2\left( {1 + \nu } \right)}}\frac{{{\partial ^2}N}}{{\partial y\partial z}}\\ {\tau _{xy}} = - \left[ {\nu {\nabla ^2} - \frac{{{\partial ^2}}}{{\partial {z^2}}}} \right]\frac{{{\partial ^2}L}}{{\partial x\partial y}} - \frac{E}{{2\left( {1 + \nu } \right)}}\left( {\frac{{{\partial ^2}}}{{\partial {x^2}}} - \frac{{{\partial ^2}}}{{\partial {y^2}}}} \right)N \end{array} $ | (7) |
把L=L(x, y, z)和N=N(x, y, z)写成分离变量的形式:
| $ \begin{array}{l} L\left( {x,y,z} \right) = \sum\limits_{m,n = 1}^\infty {{\psi _{mn}}\left( z \right)\sin \left( {{\alpha _m}x} \right)\sin \left( {{\beta _n}y} \right)} \\ N\left( {x,y,z} \right) = \sum\limits_{m,n = 1}^\infty {{\varphi _{mn}}\left( z \right)\cos \left( {{\alpha _m}x} \right)\cos \left( {{\beta _n}y} \right)} \end{array} $ | (8) |
并且有
| $ {\alpha _m} = \frac{{m{\rm{ \mathit{ π} }}}}{{{L_1}}},{\beta _n} = \frac{{n{\rm{ \mathit{ π} }}}}{{{L_2}}} $ | (9) |
式中,m和n是正整数。
将(8)代入(5)和(6)可以得到关于ψmn和φmn两个微分方程:
| $ \begin{array}{l} \frac{{{{\rm{d}}^4}{\psi _{mn}}}}{{{\rm{d}}{z^4}}} - 2\frac{{E'}}{E}\frac{{{{\rm{d}}^3}{\psi _{mn}}}}{{{\rm{d}}{z^3}}} + \left[ {2{{\left( {\frac{{E'}}{E}} \right)}^2} - \frac{{E''}}{E} - 2\lambda } \right]\frac{{{{\rm{d}}^2}{\psi _{mn}}}}{{{\rm{d}}{z^2}}} + \\ 2\frac{{E'}}{E}\lambda \frac{{{\rm{d}}{\psi _{mn}}}}{{{\rm{d}}z}} + \left\{ {\lambda + \frac{\nu }{{1 - \nu }}\left[ {2{{\left( {\frac{{E'}}{E}} \right)}^2} - \frac{{E''}}{E}} \right]} \right\}\lambda {\psi _{mn}} = 0 \end{array} $ | (10) |
| $ \frac{{{{\rm{d}}^2}{\varphi _{mn}}}}{{{\rm{d}}{z^2}}} + \frac{{E'}}{E}\frac{{{\rm{d}}{\varphi _{mn}}}}{{{\rm{d}}z}} - \lambda {\varphi _{mn}} = 0 $ | (11) |
式中,
| $ \lambda = {\lambda _{mn}} = \alpha _m^2 + \beta _n^2 $ | (12) |
若将板上下表面边界条件展开成双重傅立叶级数形式:
| $ \begin{array}{l} {Z_0}\left( {x,y} \right) = \sum\limits_{m,n = 1}^\infty {{{\bar Z}_{0mn}}\sin \left( {{\alpha _m}x} \right)\sin \left( {{\beta _n}y} \right)} \\ {Z_1}\left( {x,y} \right) = \sum\limits_{m,n = 1}^\infty {{{\bar Z}_{1mn}}\sin \left( {{\alpha _m}x} \right)\sin \left( {{\beta _n}y} \right)} \\ {X_0}\left( {x,y} \right) = \sum\limits_{m,n = 1}^\infty {{{\bar X}_{0mn}}\cos \left( {{\alpha _m}x} \right)\sin \left( {{\beta _n}y} \right)} \\ {X_1}\left( {x,y} \right) = \sum\limits_{m,n = 1}^\infty {{{\bar X}_{1mn}}\cos \left( {{\alpha _m}x} \right)\sin \left( {{\beta _n}y} \right)} \\ {Y_0}\left( {x,y} \right) = \sum\limits_{m,n = 1}^\infty {{{\bar Y}_{0mn}}\sin \left( {{\alpha _m}x} \right)\cos \left( {{\beta _n}y} \right)} \\ {Y_1}\left( {x,y} \right) = \sum\limits_{m,n = 1}^\infty {{{\bar Y}_{1mn}}\sin \left( {{\alpha _m}x} \right)\cos \left( {{\beta _n}y} \right)} \end{array} $ | (13) |
式中,
| $ \begin{array}{l} {{\bar Z}_{0mn}} = \frac{1}{{4ab}}\int_0^a {\int_0^b {{Z_0}\left( {x,y} \right)\sin \left( {{\alpha _m}x} \right)\sin \left( {{\beta _n}y} \right){\rm{d}}x{\rm{d}}y} } \\ {{\bar Z}_{1mn}} = \frac{1}{{4ab}}\int_0^a {\int_0^b {{Z_1}\left( {x,y} \right)\sin \left( {{\alpha _m}x} \right)\sin \left( {{\beta _n}y} \right){\rm{d}}x{\rm{d}}y} } \\ {{\bar X}_{0mn}} = \frac{1}{{4ab}}\int_0^a {\int_0^b {{X_0}\left( {x,y} \right)\cos \left( {{\alpha _m}x} \right)\sin \left( {{\beta _n}y} \right){\rm{d}}x{\rm{d}}y} } \\ {{\bar X}_{1mn}} = \frac{1}{{4ab}}\int_0^a {\int_0^b {{X_1}\left( {x,y} \right)\cos \left( {{\alpha _m}x} \right)\sin \left( {{\beta _n}y} \right){\rm{d}}x{\rm{d}}y} } \\ {{\bar Y}_{0mn}} = \frac{1}{{4ab}}\int_0^a {\int_0^b {{Y_0}\left( {x,y} \right)\sin \left( {{\alpha _m}x} \right)\cos \left( {{\beta _n}y} \right){\rm{d}}x{\rm{d}}y} } \\ {{\bar Y}_{1mn}} = \frac{1}{{4ab}}\int_0^a {\int_0^b {{Y_1}\left( {x,y} \right)\sin \left( {{\alpha _m}x} \right)\cos \left( {{\beta _n}y} \right){\rm{d}}x{\rm{d}}y} } \end{array} $ | (14) |
由边界条件(2)可得ψmn和φmn为:
| $ \begin{array}{l} {\psi _{mn}}\left( 0 \right) = \frac{{{{\bar Z}_{0mn}}}}{{\lambda _{mn}^2}},\;\;\;{\psi _{mn}}\left( h \right) = \frac{{{{\bar Z}_{1mn}}}}{{\lambda _{mn}^2}}\\ \frac{{{\rm{d}}{\psi _{mn}}}}{{{\rm{d}}z}}\left| {_{z = 0}} \right. = \frac{1}{{\lambda _{mn}^2}}\left( {{{\bar X}_{0mn}}{\alpha _m} + {{\bar Y}_{0mn}}{\beta _n}} \right)\\ \frac{{{\rm{d}}{\psi _{mn}}}}{{{\rm{d}}z}}\left| {_{z = h}} \right. = \frac{1}{{\lambda _{mn}^2}}\left( {{{\bar X}_{1mn}}{\alpha _m} + {{\bar Y}_{1mn}}{\beta _n}} \right) \end{array} $ | (15) |
| $ \begin{array}{l} \frac{{{\rm{d}}{\varphi _{mn}}}}{{{\rm{d}}z}}\left| {_{z = 0}} \right. = - \frac{{2\left( {1 + \nu } \right)}}{{E{\lambda _{mn}}}}\left( {{{\bar X}_{0mn}}{\beta _n} - {{\bar Y}_{0mn}}{\alpha _m}} \right)\\ \frac{{{\rm{d}}{\varphi _{mn}}}}{{{\rm{d}}z}}\left| {_{z = h}} \right. = - \frac{{2\left( {1 + \nu } \right)}}{{E{\lambda _{mn}}}}\left( {{{\bar X}_{1mn}}{\beta _n} - {{\bar Y}_{1mn}}{\alpha _m}} \right) \end{array} $ | (16) |
在边界条件(15)和(16)下求变系数常微分方程(10)与(11)的解,问题就解决了。
3 幂函数梯度分布假定弹性模量沿厚度方向按照幂函数形式变化:
| $ E\left( z \right) = {E_0}{\left( {1 + cz} \right)^p} $ | (17) |
式中,c和p是两个材料常数,用来描述E(z)的非均匀性。将(17)带入(10)和(11),可以得到:
| $ \begin{array}{l} \frac{{{{\rm{d}}^4}{\psi _{mn}}}}{{{\rm{d}}{z^4}}} - \frac{{2cp}}{{1 + cz}}\frac{{{{\rm{d}}^3}{\psi _{mn}}}}{{{\rm{d}}{z^3}}} + \left[ {\frac{{p{c^2}\left( {p + 1} \right)}}{{{{\left( {1 + cz} \right)}^2}}} - 2\lambda } \right]\frac{{{{\rm{d}}^2}{\psi _{mn}}}}{{{\rm{d}}{z^2}}} + \\ \frac{{2pc\lambda }}{{1 + cz}}\frac{{{\rm{d}}{\psi _{mn}}}}{{{\rm{d}}z}} + \left[ {\lambda + \frac{{v\left( {p + 1} \right){c^2}p}}{{\left( {1 - v} \right){{\left( {1 + cz} \right)}^2}}}} \right]\lambda {\psi _{mn}} = 0 \end{array} $ | (18) |
| $ \frac{{{{\rm{d}}^2}{\varphi _{mn}}}}{{{\rm{d}}{z^2}}} + \frac{{pc}}{{1 + cz}}\frac{{{\rm{d}}{\varphi _{mn}}}}{{{\rm{d}}z}} - \lambda {\varphi _{mn}} = 0 $ | (19) |
方程(18)的解为:
对于
| $ \begin{array}{*{20}{c}} {{\psi _{mn}} = {z_1}^{g - 1/2}\left[ {{A_1}{W_{\chi ,g}}\left( {2\eta {z_1}} \right) + {A_2}{W_{ - \chi ,g}}\left( {2\eta {z_1}} \right) + } \right.}\\ {\left. {{A_3}{W_{\chi ,g}}\left( { - 2\eta {z_1}} \right) + {A_4}{W_{ - \chi ,g}}\left( { - 2\eta {z_1}} \right)} \right]} \end{array} $ | (20) |
对于
| $ \begin{array}{l} {\psi _{mn}} = {z_1}^g\left\{ {{A_1}{I_g}\left( {\eta {z_1}} \right) + {A_2}{K_g}\left( {\eta {z_1}} \right) + } \right.\\ {A_3}\left[ {{I_g}\left( {\eta {z_1}} \right)\int {K_g^2\left( {\eta {z_1}} \right)d{z_1}} - } \right.\\ \left. {{K_g}\left( {\eta {z_1}} \right)\int {{I_g}\left( {\eta {z_1}} \right){K_g}\left( {\eta {z_1}} \right)d{z_1}} } \right] + \\ {A_4}\left[ {{I_g}\left( {\eta {z_1}} \right)\int {{I_g}\left( {\eta {z_1}} \right){K_g}\left( {\eta {z_1}} \right)d{z_1}} - } \right.\\ \left. {\left. {{K_g}\left( {\eta {z_1}} \right)\int {I_g^2\left( {\eta {z_1}} \right)d{z_1}} } \right]} \right\} \end{array} $ | (21) |
方程(19)的解为:
| $ {\varphi _{mn}} = {z_1}^{ - g + \frac{3}{2}}\left[ {{B_1}{I_{ - g + 3/2}}\left( {\eta {z_1}} \right) + {B_2}{K_{ - g + 3/2}}\left( {\eta {z_1}} \right)} \right] $ | (22) |
并且
| $ \chi = \frac{1}{2}\sqrt {\left( {p + 1} \right)\left( {1 - \frac{{vp}}{{1 - v}}} \right)} $ | (23) |
式中, W±χ, g(±2ηz1)是Whittaker函数, Ig(ηz1)和Kg(ηz1)分别是第一类和第二类g阶修正贝赛尔函数, I-g+3/2(ηz1)和K-g+3/2(ηz1)分别是第一类和第二类-g+3/2阶修正贝赛尔函数,系数A1, A2, A3, A4, B1, B2可以通过边界条件(15)和(16)求得。
4 算例与讨论考虑一个四边简支功能梯度材料方板,L1=L2=1 m,h=0.1 m,上下表面作用的荷载为
| $ \begin{array}{l} {Z_1}\left( {x,y} \right) = - q\sin \left( {\frac{{\rm{ \mathit{ π} }}}{a}x} \right)\sin \left( {\frac{{\rm{ \mathit{ π} }}}{b}y} \right),q = 1{\rm{Pa}}\\ {X_0}\left( {x,y} \right) = {Y_0}\left( {x,y} \right) = {Z_0}\left( {x,y} \right) = {X_1}\left( {x,y} \right) = {Y_1}\left( {x,y} \right) = 0 \end{array} $ |
这里取m=1,n=1,板的上下表面的弹性模量为E(0)=1 GPa,E(h)=10 GPa,在方程(17)中,p=-2, -1, 0, 1, 2,E0=E(0),
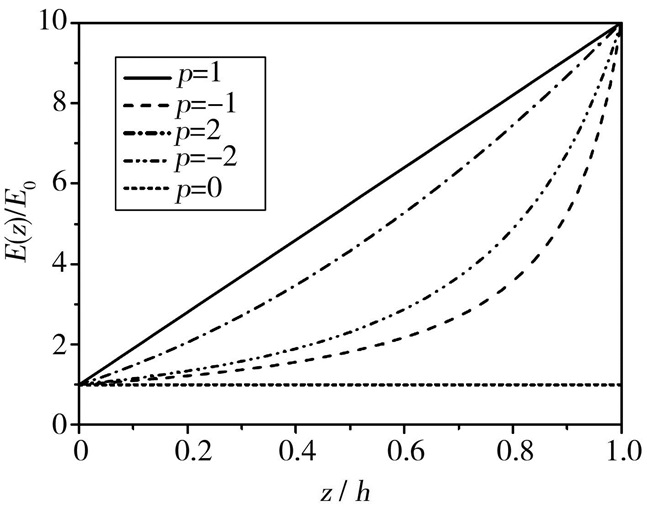
当E(h)/E(0)=10,选择不同的非均匀系数p,弹性模量沿着板厚方向的变化如图 2所示。
|
| 图 2 弹性模量沿着板厚方向的变化示意图 Figure 2 Variation of Young's modulus along thickness of plate |
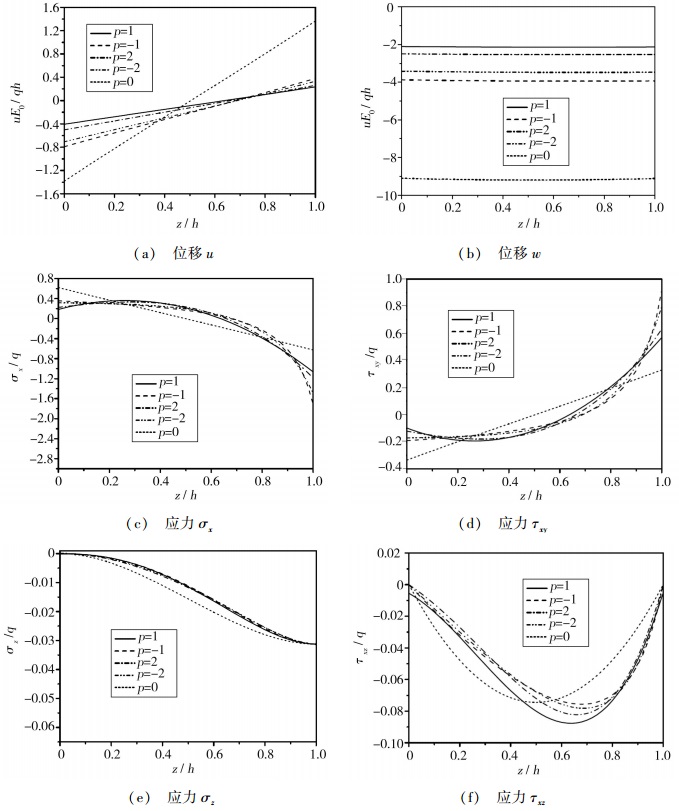
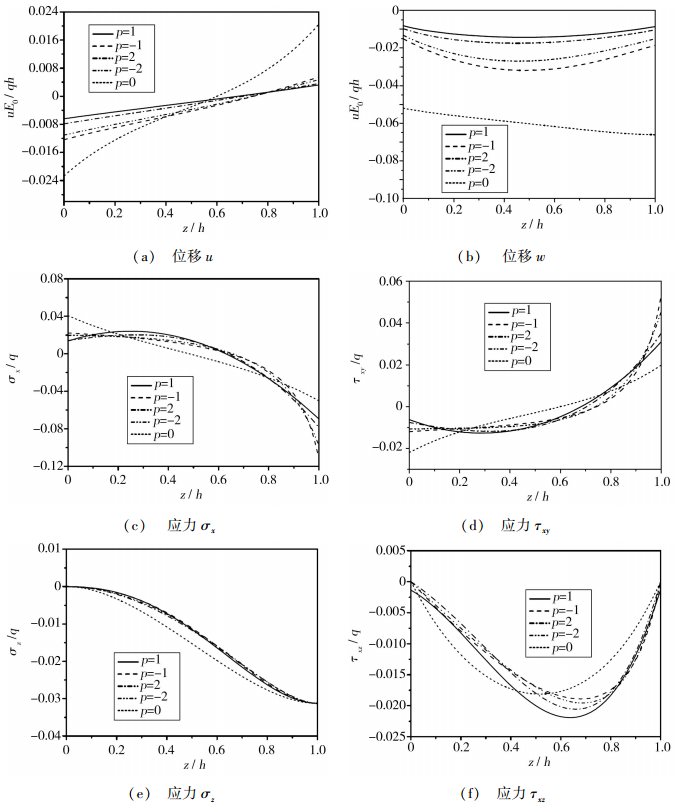
基于上面的弹性模量的几种模型,对于薄板(h/L1=0.1)和厚板(h/L2=0.4),在选定的点(x/L1=0.25,y/L2=0.25)处,位移u和w,应力σx,τxy,σz和τxz,沿着厚度方向的变化如图 3和图 4所示。由于问题的对称性,位移v,应力σy和τyz沿着板厚方向的变化图没有出现,是因为它们的变化特性分别与u,σx和τzx的变化相似。
|
| 图 3 对于薄板h/L1=0.1,在点(x/L1=0.25, y/L2=0.25)处,各个物理量沿着板厚度方向的变化图 Figure 3 Variation of physical quantities with z-coordinate at a chosen location (x/a=0.25, y/b=0.25) for a thin plate (h/a=0.1) |
|
| 图 4 对于厚板h/L1=0.4,在点(x/L1=0.25,y/L2=0.25)处,各个物理量沿着板厚度方向的变化图 Figure 4 Variation of physical quantities with z-coordinate at a chosen location (x/a=0.25, y/b=0.25) for a thick plate (h/a=0.4) |
对于一个功能梯度材料薄板,从图 3(a)和图 3(b)可以看出,位移w沿着板厚度方向的变化是基本一样的,位移u沿着板厚度方向是呈线性变化。而对于一个功能梯度材料厚板,从图 4(a)和图 4(b)可以看出,位移w沿着板厚的变化不再一致且位移u沿着板厚的变化也同线性变化相背离。
从图 3(b)和4(b)中可以看到,无论是薄板还是厚板,其竖向位移的值,在梯度模型p=1时是最小的,p=0时是最大的。这一点可以用来解释一个事实,那就是对于不同的梯度模型来说,板的弯曲刚度是不同的。另外,也能看出,对于同样的梯度模型来讲,由于薄板的弯曲刚度小于厚板,因此,薄板与厚板相比,薄板中会产生较大的变形。
从图 3(c)和图 4(c)可以看出,对于不同的弹性模量梯度模型来说,板上的面内应力分布是明显不一样的。功能梯度材料的梯度参数该如何选择,这点提供了一个设计参考。
对于一个功能梯度材料薄板来说,面外应力σz和τzx与面内应力σx相比,其大小是可以忽略的。但是对于一个厚板来说,这点是不成立的,由于σz和τzx与σx的大小是较接近的。这点在建立简化的功能梯度材料薄板理论时可以加以考虑。
5 结论给出了上下表面任意荷载作用下四边简支功能梯度板弯曲问题的解析解,其中假设材料弹性模量在板厚度方向上呈幂函数梯度分布。通过算例分析,得到双三角函数形式荷载作用下功能梯度矩形板的应力和位移分量。讨论了非均匀参数的变化对板应力和位移场的影响。该方法为发展针对功能梯度材料特点的数值算法和简化理论提供依据。
| [1] | KIEBACKB, NEUBRAND A, RIEDEL H. Processing techniques for functionally graded materials[J]. Mater. Sci. Eng. A, 2003, 362: 81–105. |
| Click to display the text | |
| [2] | 王保林, 韩杰才, 张幸红. 非均匀材料力学[M]. 北京: 科学出版社, 2003. |
| [3] | MIYAMOTO, Y, KAYSSER, W A, RABIN, B H, et al. Functionally graded materials: design processing and applications[M]. Kluwer Academic, Boston, 1999. |
| [4] | KASHTALYAN M. Three-dimensional elasticity solution for bending of functionally graded rectangular plates[J]. Eur. J. Mech. A. Solids, 2004, 23: 853–864. |
| Click to display the text | |
| [5] | ZHONG Z, SHANG E T. Closed-Form solutions of three-dimensional functionally graded plates[J]. Mech. Adv. Mater. Struct., 2008, 15: 355–363. |
| Click to display the text | |
| [6] | YANG B, DING J H, CHEN W Q. Elasticity solutions for functionally graded rectangular plates with two opposite edges simply supported[J]. Applied Mathematical Modelling, 2012, 36: 488–503. |
| Click to display the text | |
| [7] | YOSHIHIRO O, MASAYUKI I. Three-dimensional solution for transient thermoelastic problem of a functionally graded rectangular plate with piecewiseexponential law[J]. Composite Structures, 2013, 106: 672–680. |
| Click to display the text | |
| [8] | ABALI B E, VöLLMECKE C, WOODWARD B, et al. Three-dimensional elastic deformation of functionally graded isotropic plates under point loading[J]. Composite Structures, 2014, 118: 367–376. |
| Click to display the text | |
| [9] |
周凤玺, 李世荣. 功能梯度材料矩形板的三维瞬态热弹性分析[J].
工程力学, 2009, 26(8): 59–64.
|
| Cited By in Cnki (3) | |
| [10] |
余莲英, 张亮亮, 尚兰歌, 等. 功能梯度曲梁弯曲问题的解析解[J].
工程力学, 2014, 31(12): 4–10.
|
| Cited By in Cnki (1) | |
| [11] | WOODWARD B, KASHTALYAN M. A piecewise exponential model for three-dimensional analysis of sandwich panels with arbitrarily graded core[J]. International Journal of Solid and Structures, 2015, 75-76: 188–198. |
| Click to display the text | |
| [12] |
杨智勇, 牛忠荣, 程长征, 等. 功能梯度矩形板问题三维理论的半解析解[J].
应用力学学报, 2013, 30(4): 581–586.
|
| Cited By in Cnki (2) | |
| [13] | PRADHAN K K, CHAKRAVERTY S. Static analysis of functionally graded thin rectangular plates with various boundary supports[J]. Archives of Civila and Mechanical Engineering, 2015, 15: 721–734. |
| Click to display the text | |
| [14] | MANTARI J L, RAMOS I A, CARRERA E, et al. Static analysis of functionally graded plates using new nonpolynomial displacement fields via carrera unified formulation[J]. Composites Part B, 2016, 89: 127–142. |
| Click to display the text | |
| [15] | PLEVAKO V P. On the theory of elasticity of inhomogeneous media[J]. Appl. Math. Mech., 1971, 35: 806–813. |
| Click to display the text | |
| [16] | ZHONG Z, SHANG E T. Closed-form solutions of three-dimensional functionally graded plates[J]. Mechanics of Advanced Materials and Structures, 2008, 15(5): 355–363. |
| Click to display the text |


