雷达隐身技术是现代战争中最重要、最有效的突防技术手段。可通过外形设计和使用吸波材料对武器装备进行隐身设计。而单一的吸波材料结构存在着电磁参数可调范围小、频响特性差、吸收频带窄等问题,不能满足隐身技术对轻质宽频的要求;理想的吸波材料应具有厚度薄、质量轻、吸收频带宽、吸波能力强(薄、轻、宽、强)等特点,多层结构吸波材料可通过设计灵活度弥补材料本身的缺陷,能在一定程度上降低面密度有效改善吸波效果,拓宽材料吸波带宽[1-5]。本文介绍了多层结构吸波材料设计的理论模型及优化设计方法,论述了多层结构设计对吸波材料性能的影响,展望了多层结构吸波材料的发展趋势。
1 多层结构吸波材料的理论模型及优化设计方法 1.1 理论模型材料的吸波性能通常以反射率表示,反射率为负值,其值越小,表明其吸波性能越好。根据电磁场理论,可用复介电常数ε和复数磁导率μ以及材料厚度d来表征其反射率,典型的理论模型为传输线理论[6]。等效传输线法是目前应用最广的一种多层材料反射系数求解方法,该方法利用传输线理论导出多层涂层反射系数,具有计算简洁的优点。多层材料结构示意图见图 1,图 1中右方最底端为金属板,即全反射板,电磁波由左侧垂直入射到吸波材料上。假设第i层为均质、等厚平板吸波材料,则n层平板吸波材料的综合吸波性能可以用(1)~(6) 式表示。
| $ {\gamma _i} = {\rm{j}}\frac{{2{\rm{\pi }}f}}{{\rm{c}}}\sqrt {{\mu _i}{\varepsilon _i}} $ | (1) |
| $ {\eta _i} = \sqrt {\frac{{{{\mu '}_i} - {\rm{j}}{{\mu ''}_i}}}{{{{\varepsilon '}_i} - {\rm{j}}{{\varepsilon ''}_i}}}} \cdot \sqrt {\frac{{{\mu _0}}}{{{\varepsilon _0}}}} $ | (2) |
| $ {Z_{{\rm{in}}}}\left( i \right) = {\eta _i}\frac{{{Z_{{\rm{in}}}}\left( {i - 1} \right) + {\eta _i}\tan h\left( {{\gamma _i}{d_i}} \right)}}{{{\eta _i} + {Z_{{\rm{in}}}}\left( {i - 1} \right)\tan h\left( {{\gamma _i}{d_i}} \right)}} $ | (3) |
| $ {Z_{{\rm{in}}}}\left( 1 \right) = {\eta _1}\tan h\left( {{\gamma _1}{d_1}} \right) $ | (4) |
| $ {\mathit{{\Gamma }}}\left( n \right){\rm{ = }}\frac{{{Z_{{\rm{in}}}}\left( n \right) - {Z_0}}}{{{Z_{{\rm{in}}}}\left( n \right) + {Z_0}}} $ | (5) |
| $ {R_{{\rm{dB}}}}\left( n \right) = 20\lg \left| {\mathit{\Gamma} \left( n \right)} \right| $ | (6) |

|
| 图 1 多层吸波材料结构示意图 Figure 1 Structure of multilayer absorbing material |
式中,Z0为自由空间的波阻抗,γi为电磁波在第i层材料的波矢,垂直入射时可视为常数,c为光速,f为入射电磁波的频率,μi=μ′i-jμ″i和εi=ε′-jε″分别为材料的复磁导率和复介电常数,ηi为第i层材料的特性阻抗,μ0为真空中的磁导率,ε0为真空中的介电常数,Zin (i)为第i层吸波材料的输入阻抗,di为第i层材料的厚度, Zin (1) 为第1层吸波材料(紧贴金属衬底)的输入阻抗,RdB(n)为反射率(负值,其绝对值的大小常用于表征材料吸波性能水平,绝对值越大则性能越优异),Γ(n)为综合反射系数。由式(1)~(6) 可见多层吸波材料的反射率可通过各层吸波材料的复介电常数磁导率,以及材料厚度,由第一层材料的输入阻抗,依次求解出面层输入阻抗,从而推导得到反射率[7-10]。
1.2 设计原则在多层结构吸波材料设计中,采用最多的是阻抗渐变原则,即自下而上,每层材料的阻抗逐渐变大(图 2),实现材料阻抗变化可通过吸收剂浓度改变或更换材料种类两种方式进行。采用阻抗渐变原则设计吸波材料类同于尖劈吸波材料(图 3),不同的是尖劈材料从物理形状上实现了阻抗的变化,多层材料结构从每层材料的电磁参数差异或含量变化实现阻抗的变化[11-16]。阻抗渐变设计材料的最大优势是可以在很宽的频率范围内实现大吸收,这一点可以从50 mm蜂窝尖劈材料的吸波性能得到验证(图 4)。在某些情况下,如在需要提高低频吸收峰时,采用阻抗逐渐变小的设计则更为有效,其主要原因在该频段产生了谐振吸收,能在某些频带出现强吸收峰,但是牺牲了吸收带宽。

|
| 图 2 阻抗渐变示意图 Figure 2 Illustration of impedance gradient change |

|
| 图 3 尖劈吸波材料示意图 Figure 3 Illustration of wedge absorbing material |

|
| 图 4 50 mm蜂窝尖劈材料反射率曲线图 Figure 4 Reflectivity of 50 mm honeycomb structured wedge absorbing material |
如图 5所示为一种双层阻抗逐渐变小的吸波材料反射率曲线,在3.36 GHz出现了强烈的吸收峰,但在-20 dB以下峰宽小于1 GHz。

|
| 图 5 某吸波材料的反射率 Figure 5 Reflectivity of an absorbing material |
多层吸波材料的吸波性能与各层的电磁常数、介电常数、厚度等参数有关,在上述参数已知的情况下,通过优化设计可预估材料吸波性能,进行材料结构层数优化设计,大幅度提高效率。遗传算法(GA)是一类借鉴生物界自然选择和自然遗传机制的随机化搜索算法,其基本思想是从一组候选解开始迭代, 在每次迭代的过程中保留其中优秀的候选解, 通过遗传操作, 如杂交、变异等运算, 产生新一代候选解。重复以上过程, 直到满足某个收敛条件为止,主要特点是群体搜索策略和群体中个体之间的信息交换,搜索不依赖于梯度信息,具有自组织、自适应和自学习功能,通过优胜劣汰的原理,达到快速收敛的目的,适于处理多层吸波材料的优化这类多参数复杂系统的设计问题[17-25]。肖刚等[26]对多层吸波材料进行遗传算法优化, 计算了2~4层材料, 得到了最优解;周志安等[27]采用了带约束条件的单目标标准遗传算法(SGA)来设计高性能的吸波涂层, 还成功的将多目标遗传算法引入到多层纳米吸波材料的设计中, 得到性能优异的多层结构吸波材料;陈良等 [28]采用混合遗传算法(模拟退火算法与遗传算法的结合),利用该方法优化的结果,可使五层平板浸炭泡沫吸波材料在宽频带范围(2~18 GHz)内平均吸收性能达到-15 dB以上。
2 多层结构设计对吸波材料性能的影响 2.1 电磁特性吸波材料种类繁多,从吸收原理来分,大致可分为两类:一是磁性吸收材料,主要以铁氧体、羰基铁、磁纤维、碳化硅等为吸收剂的材料;二是介电型吸收材料,主要以碳黑、碳纤维、碳管、金属纤维、导电高聚物等为吸收剂的材料[29-33]。
铁粉吸收剂是目前最常用、也是最有效的吸收剂,主要为羰基铁或其改性体,其优异的磁性能可使吸波材料具备厚度薄、吸收频带宽等优点,缺点是材料的密度大、防腐效果差。典型铁粉吸收剂的电磁参数见图 6。碳黑吸收剂是常用介电吸收剂之一,具有质量轻、防腐性能好的优点,缺点是材料厚度大、吸收频带窄。典型的碳黑电磁参数见图 7。

|
| 图 6 80wt%铁粉材料电磁参数 Figure 6 Electromagnetic parameter of 80wt% iron powder |

|
| 图 7 10wt%碳黑材料电磁参数 Figure 7 Electromagnetic parameter of 10wt% carbon black |
由式(1)~(3) 的推导可见,材料吸波性能为电磁参数(ε=ε′-jε″、μ=μ′-jμ″)、频率f以及厚度d的函数,在实际应用过程中,涂层厚度为一定量值,如果在一定的频率范围内需要良好的吸收性能,由式(4)~(6) 可知,必然要求其电磁参数随着频率的变化而变化,形成频散效应,保证输入阻抗的稳定或升高,从而具有宽频带吸波性能。从图 6可见,对铁粉类吸收剂材料而言,介电常数随频率变化不大,但是其磁导率和磁损耗有较好的频率响应特性,因此该类涂层吸收带宽较大。
图 8为该铁粉材料在不同厚度时的仿真反射率,结果显示,随着涂层厚度的增加,反射率逐渐倾向于成为一条平线,且在厚度超过6 mm以后,反射率不再发生明显变化,全频段位于-8.5 dB左右。实际应用中,一般在高频(8~18 GHz)要求10 dB吸收时,单层铁粉材料可以实现,但如果吸收性能要求更高时,则需要材料本身的电磁参量随频率变化幅度应更大才能满足设计要求,现实中材料不具备该种特性,因此需考虑采取多层结构设计方案,采用不同参数的吸波材料实现大幅度的磁导率和磁损耗变化。图 7所示碳黑类吸收剂作为介电类材料其磁导率与磁损耗基本符合理论值(μ′=1,μ″=0),其介电常数随频率变化仅有小幅变动,所以该类材料反射率呈现单一的吸收峰,如图 9所示,且随着厚度增加,吸收峰向低频偏移,无法满足宽频吸收要求,因此介电类材料宽带设计也需采用多层结构或改变材料的频率响应特性才可满足宽带吸收性能。

|
| 图 8 不同厚度80wt%铁粉材料的反射率 Figure 8 Reflectivity of different thickness of 80wt% iron powder |

|
| 图 9 不同厚度10wt%碳黑材料的反射率 Figure 9 Reflectivity of different thickness of 10wt% carbon black |
吸波材料多层结构设计从本质上来讲,是将材料厚度分成若干层,每层可设置不同的电磁参数,从宏观上引入材料参数变化梯度,增加参数调整的灵活度,对吸波性能影响表现在以下几方面。
2.2.1 拓宽吸收频带宽带吸收的本质是对材料(单层或多层)等效电磁参数频响特性进行调整,其调整幅度大小及变化趋势决定了材料吸收性能,而多层设计正是由于从厚度方向引入了不同参数的材料,具备调整等效参数的功能,因此可以实现吸收频带的展宽。从目前报道中可知,何山等[34]研制的JB-5多层吸波材料,在6~17 GHz频段,反射率小于-12 dB;其研制的一种宽带轻质泡沫型吸波材料在8~18 GHz频段反射率均小于-15 dB[35]。赵宏杰等 [14]采用多层阻抗渐变设计的三层4 mm厚吸波层板在5~18 GHz频段反射率小于-10 dB;其研制的六层吸波泡沫在8~12 GHz频段反射率小于-30 dB。航天材料及工艺研究所研制的一种20 mm厚多层泡沫吸波材料在8~12 GHz频段反射率小于-30 dB,8~18 GHz频段反射率小于-20 dB(图 10)。

|
| 图 10 多层泡沫结构吸波材料反射率曲线图 Figure 10 Reflectivity of 15 mm multilayer polyfoam absorbing material |
在多层结构吸波涂层的研制过程中,仅采用表 1中1、2两种材料的双层结构时,反射率呈现窄而深的单吸收峰,如图 11中曲线① 所示。进一步优化改进为1~5五层结构后,通过引入不同电磁参数的材料,改善了材料整体的频率响应特性,使其在较宽频率范围内形成阻抗匹配,有效拓宽了多层结构吸波涂层的吸收带宽,反射率曲线如图 11中曲线② 所示,多层吸波材料在8~12 GHz频段反射率<-18 dB,且具有优异的RCS(雷达散射截面积)性能。
| 层数 | ε′ | ε″ | μ′ | μ″ | d/mm |
| 1 | 22.78 | 3.85 | 1.79 | 2.63 | 1.5 |
| 2 | 3.94 | 0.22 | 1.04 | 0.06 | 1.1 |
| 3 | 24.75 | 3.51 | 1.84 | 1.95 | 0.4 |
| 4 | 3.94 | 0.22 | 1.04 | 0.06 | 1.0 |
| 5 | 2.54 | 0.04 | 1 | 0 | 3.7 |

|
| 图 11 两种多层结构吸波涂层反射率曲线 Figure 11 Reflectivity of two multilayer absorbing coatings |
在多层结构设计中,往往会引入介质层(低介电损耗材料)作为匹配层来调整材料等效参数,介质层一般为含有空气的材料,如空心玻璃微球、酚醛微球、泡沫材料等,该类材料一般密度较小,引入后具有降低等效电磁参数、增大频响幅度的特性,从而改善材料吸波性能。实际测试结果表明,在相同厚度和吸波性能的情况下,引入介质层能降低材料的面密度,如1.0 mm涂层在8~18 GHz达到8 dB吸收时,无介质层时其面密度为3.6~3.7 kg/m2,而引入介质层后面密度降低0.3~0.4 kg/m2。
2.2.3 提高吸收峰值窄带大吸收类吸波材料常用于解决电磁干扰问题,其吸收带宽一般在1 GHz范围内,吸收性能则要求大于20 dB,而要实现此吸收效果,材料的介电损耗须尽可能小,从而能与自由空间的波阻抗进行匹配[36],而不至于在电磁波未能进入材料内部而在表面产生大量反射,在多层设计中,介质层正好具有降低材料等效介电损耗的特性,因此可用于提高材料的吸收峰值。天津大学以短切活性碳纤维作为吸收剂设计的4 mm厚四层吸波材料,在2~18 GHz频段内反射率达到-10 dB以下的频带宽度为8 GHz,最大反射衰减-39.3 dB[37]。航天材料及工艺研究所的多层泡沫结构吸波材料通过将参数特性接近于自由空间的泡沫材料A[图 12(a)]和吸波材料B[图 12(b)]进行复合优化设计。

|
| 图 12 泡沫材料A和吸波材料B的电磁参数 Figure 12 Electromagnetic parameter of A polyfoam and B absorbing material |
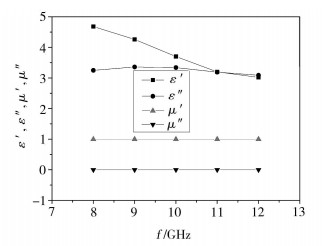
将泡沫材料A与吸波材料B按照厚度比5:1复合后,得到的复合材料C(等效电磁参数见图 13),从材料电磁参数变化可见,通过加入介质层(泡沫材料),吸波材料的厚度增加,但使材料的ε′及ε″均大幅度下降;图 14为A、B材料复合前后的反射率变化,A、B在复合之前,反射率均趋于0,通过复合设计后,在8~12 GHz反射率达到-8 dB。可见通过与介质材料复合设计有利于多层结构吸波材料设计中材料参数调整,促进吸波性能的提升。
|
| 图 13 复合吸波材料C的电磁参数 Figure 13 Electromagnetic parameter of C composite absorbing material |

|
| 图 14 A, B, C的反射率曲线 Figure 14 Reflectivity of A, B, C |
多层结构吸波材料设计是与每层材料的电磁参数和厚度相关,而且相互影响的多目标设计问题,故在设计制造过程中,存在以下技术难点:(1) 多层结构吸波材料涉及多种材料、多种厚度的匹配设计,相较于单层材料,其工艺容差性小,累计误差大,由实际测试结果与模拟结果比较,反馈优化调节是其一大难点;(2) 设计过程中的测量误差易产生累计放大,故制造过程中需要严格的工艺精细化控制,执行最优设计厚度;(3) 多层结构材料层间界面多,材料种类不一,使材料其他性能(如附着力、粘接性能、韧性、界面应力等)的影响复杂化,界面相容性问题突出,同时需要兼顾工艺流程及可行性。
随着隐身材料技术的长足发展,材料种类增多、层数增加、应用复合化,多层结构吸波材料将呈现出多样化、复杂化发展态势。此外,多层结构设计技术作为实现吸波材料宽频段、大吸收的一条主要技术途径,未来多层结构设计将依赖于吸波理论模型的优化发展,计算机辅助设计系统的应用,以及材料制造工艺技术水准的提升,三者共同推动复杂结构吸波材料的工程化应用,促进隐身材料技术的发展。
| [1] |
张月芳, 郝万军. 吸波材料研究进展及其对军事隐身技术的影响[J].
化工新型材料, 2012(1): 13–15.
|
| Cited By in Cnki (29) | |
| [2] |
张健, 张文彦, 奚正平. 隐身吸波材料的研究进展[J].
稀有金属材料与工程, 2008(S4): 504–508.
|
| Cited By in Cnki (72) | |
| [3] |
刘献明, 付绍云, 张以河, 等. 雷达隐身复合材料的进展[J].
航空电子技术, 2004(2): 31–36.
|
| Cited By in Cnki (9) | |
| [4] |
唐恩凌, 王崇. 纳米雷达隐身吸波材料[J].
飞航导弹, 2009(3): 57–60.
|
| Cited By in Cnki (18) | |
| [5] |
李斌玲, 谢国治, 宋晓龙, 等. 多层雷达波段吸波涂层的研究现状及展望[J].
河海大学学报(自然科学版), 2011(4): 464–469.
|
| Cited By in Cnki (4) | |
| [6] | BRONWELL A. Transmission-Line Analogies of Plane Electromagnetic-Wave Reflections[J]. Proceedings of the Ire, 1944, 32(4): 233–241. |
| Click to display the text | |
| [7] |
唐宏, 赵晓鹏, 邢丽英, 等. 多层吸波材料的数值优化设计[J].
微波学报, 2003(3): 55–58.
|
| Cited By in Cnki (33) | |
| [8] |
王俊鸣, 朱志军, 章志敏. 基于遗传算法的多层吸波材料优化设计[J].
现代雷达, 2013(11): 66–70.
|
| Cited By in Cnki (4) | |
| [9] |
魏永生, 郭玉宝, 赵新生, 等. 多层吸波材料的优化设计模型[J].
北京交通大学学报, 2015(3): 95–100.
|
| Cited By in Cnki (3) | |
| [10] | 李艳厦. 结构型吸波材料的理论研究及其优化设计[D]. 燕山大学, 2008. |
| Cited By in Cnki (4) | |
| [11] | KOSTORNOV A G, MOROZ A L, SHAPOVAL A A, et al. Composite structures with gradient of permeability to be used in heat pipes under microgravity[J]. Acta Astronautica, 2015(115): 52–57. |
| Click to display the text | |
| [12] | CHEN M, ZHU Y, PAN Y, et al. Gradient multilayer structural design of cnts/SiO2 composites for improving microwave absorbing properties[J]. Materials & Design, 2011, 32(5): 3013–3016. |
| Click to display the text | |
| [13] | TAMBURRANO A, RINALDI A, PROJIETTI A, et al. Multilayer graphene-coated honeycomb as wideband radar absorbing material at radio-frequency[C].//IEEE, International Conference on Nanotechnology, 2015. |
| [14] |
赵宏杰, 宫元勋, 邢孟达, 等. 结构吸波材料多层阻抗渐变设计及应用[J].
宇航材料工艺, 2015, 45(4): 19–22, 34.
|
| Cited By in Cnki (5) | |
| [15] | 冯彬. 层板结构吸波复合材料吸波性能研究[D]. 武汉理工大学, 2010. |
| Cited By in Cnki (4) | |
| [16] | 吕述平. 微波暗室用谐振型角锥吸波材料的研究[D]. 大连理工大学, 2006. |
| Cited By in Cnki (6) | |
| [17] |
亓家钟, 陈倍京, 陈利民. 多层吸波材料反射损失计算机模拟[J].
金属功能材料, 2006(2): 33–36.
|
| Cited By in Cnki (10) | |
| [18] |
袁杰, 王荣国, 李颖慧, 等. 多层吸波材料的计算机辅助优化设计[J].
哈尔滨工程大学学报, 2000(2): 51–54.
|
| Cited By in Cnki (34) | |
| [19] |
何山, 熊克敏. 雷达罩内用泡沫型吸波材料研究[J].
航空材料学报, 2001(3): 19–23.
|
| Cited By in Cnki (15) | |
| [20] | PESQUE J J, BOUCHE D, MITTRA R, et al. Optimization of multilayer antireflection coatings using an optimal control method[J]. IEEE Transactions on Microwave Theory and Techniques, 1992, 40(9): 1789–1796. |
| Click to display the text | |
| [21] |
王晨, 顾家琳, 康飞宇. 吸波材料理论设计的研究进展[J].
材料导报, 2009(5): 5–8.
|
| Cited By in Cnki (35) | |
| [22] | WEILE D S, MICHIELSSEN E. Genetic algorithm optimization applied to electromagnetics:a review[J]. IEEE Transactions on Antennas & Propagation, 1997, 45(3): 343–353. |
| Click to display the text | |
| [23] | CHEN X, LIU XX, WANG XJ, et al. Optimized design for multi-layer absorbing materials based on genetic algorithm[J]. Advanced Materials Research, 2013, 681: 324–328. |
| Click to display the text | |
| [24] | POLI R, KENNEDY J, BLACKWELL T. Particle swarm optimization[C]//Swarm Intelligence Symposium, 2007. SIS 2007. IEEE. IEEE, 2007:120-127. |
| [25] | EBERHART R, KENNEDY J. A new optimizer using particle swarm theory[C].//International Symposium on MICRO Machine and Human Science. IEEE, 1995:39-43. |
| [26] | 肖钢. 多层吸波材料计算设计及优化研究[D]. 哈尔滨工程大学, 2003. |
| Cited By in Cnki (7) | |
| [27] | 陈良. 多层宽带泡沫吸波材料的遗传算法优化设计与制备[D]. 电子科技大学, 2001. |
| Cited By in Cnki (1) | |
| [28] | 周志安. 多层纳米吸波材料的遗传优化设计及数值计算[D]. 南京理工大学, 2008. |
| Cited By in Cnki (8) | |
| [29] |
赵灵智, 胡社军, 李伟善, 等. 吸波材料的吸波原理及其研究进展[J].
现代防御技术, 2007(1): 27–31+48.
|
| Cited By in Cnki (148) | |
| [30] |
张健, 张文彦, 奚正平. 隐身吸波材料的研究进展[J].
稀有金属材料与工程, 2008(S4): 504–508.
|
| Cited By in Cnki (72) | |
| [31] |
李瑞琦, 何世禹, 初文毅. 吸波涂层材料研究进展[J].
兵器材料科学与工程, 2006(3): 76–80.
|
| Cited By in Cnki (39) | |
| [32] |
程涛, 李铁虎, 李莎莎, 等. 吸波材料的研究进展[J].
材料导报, 2011(15): 50–52+63.
|
| Cited By in Cnki (14) | |
| [33] | SINGH P, BABBAR V K, RAZDAN A, et al. Complex permittivity, permeability, and X-band microwave absorption of CaCoTi ferrite composites[J]. Journal of Applied Physics, 2000, 87(9): 4362–4366. |
| Click to display the text | |
| [34] |
李清岩, 杨东方. 遗传算法在雷达吸波涂层多目标优化设计中的应用[J].
航空材料学报, 2007(3): 82–86.
|
| Cited By in Cnki (6) | |
| [35] |
何山, 李业华, 周淳. 一种多层胶板雷达吸波材料[J].
航空材料学报, 2016(4): 41–46.
|
| Cited By in Cnki (1) | |
| [36] |
张铁夫, 曹茂盛, 袁杰, 等. 多薄层涂覆吸波材料计算设计方法研究[J].
航空材料学报, 2001(4): 46–49+62.
|
| Cited By in Cnki (27) | |
| [37] | 邹田春. 活性碳纤维(毡)/环氧树脂吸波复合材料的设计与吸波性能的研究[D]. 天津大学, 2007. |
| Cited By in Cnki (13) |


